2020年山东省菏泽市教师招聘考试题(数学)
分类:教师公开招聘/山东 来源:fenbi
一、单项选择题。本大题共7小题,每题2分,共14分
1
设集合,
,则下列关系中正确的是( )。
A、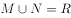
B、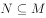
C、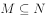
D、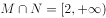
2
已知曲线,则曲线C( )。
A、关于x轴对称
B、关于坐标原点对称
C、关于y轴对称
D、关于直线y=x对称
3
从分别标有的8个球中,任取2个球,这2个球上的字母顺序不相邻的概率为( )。
A、
B、
C、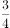
D、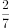
4
已知双曲线(
),
为其一个顶点,
、
为其左右焦点。以A为圆心,c为半径的圆与双曲线E的一条渐近线,交于P、Q两点,若
,则下列选项正确的是( )。
A、渐近线方程为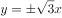
B、曲线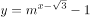 (
(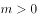 ,且
,且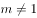 )经过双曲线E的一个焦点
)经过双曲线E的一个焦点
C、离心率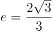
D、直线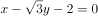 与曲线E有两个公共点
与曲线E有两个公共点
5
已知是正数,若
,则
的取值范围为( )。
A、{1}
B、{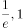 }
}
C、{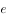 }
}
D、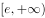
6
若复数(
,
为复数单位)模为2,且
,则
的取值范围为( )。
A、
B、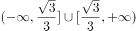
C、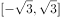
D、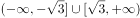
7
经过点,且与直线
和直线
垂直的直线方程为( )。
A、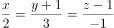
B、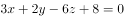
C、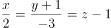
D、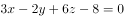
二、填空题。本大题共8小题,每题2分,共16分
8
若,则
的值为______。
9
若曲线关于直线
对称的图形仍是其本身,则实数m的值为
10
过长方体同一顶点后的三条棱长度之和为,长方体的表面积为
,则该长方体外接球的表面积为______。
11
若(
)的展开式中,各项系数和与二项式系数和之差为240,则展开式中的常数项为
12
缺
13
已知函数,则不等式
的解集为______。
14
若正四面体ABCD的棱长为,设二面体A-BC-D的平面角为
,则
的正切值为______。
15
=______。
三、解答题。本大题共6小题,共70分
16
已知函数。
(1)当时,用导数定义求函数
在
处的导数;
(2)求的极值。
17
设关于x的一元二次方程,有两根
和
,且满足
,
。
(1)求数列的通项公式;
(2)令,
,求数列
的前n项和
。
18
已知椭圆的一个焦点与抛物线
的焦点重合,过W的焦点与其长轴垂直的直线被所截得线段的长度为3,过椭圆W的右焦点
,且不与坐标轴垂直的直线与椭圆W交于
两点。弦AB的中点为M,O为坐标原点,k为直线AB的斜率,
为直线OM的斜率。
(1)求椭圆W的方程;
(2)求的值;
(3)求弦AB的中点M的轨迹方程。
19
计算二重积分。
,其中D是曲线
,直线
,
所围成的区域。
20
求初值问题,
的解。
21
设矩阵,求矩阵A的特征值和特征向量。