2015上半年教师资格证考试《数学学科知识与教学能力》(初级中学)真题
分类:教师资格/初中 来源:233网校
一、(本大题共8小题,每题5分,共40分)
1
与命题 连续”不等价的命题是( )。
连续”不等价的命题是( )。
 连续”不等价的命题是( )。
连续”不等价的命题是( )。 A、

B、

C、

D、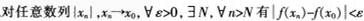
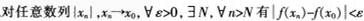
2
已知集合
 则集合M r-)N=( )。
则集合M r-)N=( )。 A、(一∞,1)
B、(一1,1]
C、Ф
D、{1}
3
 成立的( )。
成立的( )。 A、充分条件但不是必要条件
B、充分必要条件
C、必要条件但不是充分条件
D、以上都不是
4
设x=a是代数方程f(x)=0的根,则下列结论不正确的是( )。
A、 叫是f(x)的因式
B、X-a整除f(x)
C、(a,0)是函数y=f(x)的图象与2轴的交点
D、 f(a)=0
5
三次函数r=ax3+bx2+cx+d的导函数图象如图1,

则此三次函数的图象是( )。
A、 

B、

C、

D、 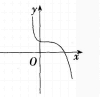

6
直线

与平面π:x+y+z=2的位置关系是( )。
A、平行
B、相交但不垂直
C、垂直
D、直线f在平面上
7
义务教育阶段的数学课程应该具有( )。
A、基础性、普及性、发展性
B、实践性、普及性、选拔性
C、基础性、实践性、选拔性
D、实践性、普及性、发展性
8
下面是关于学生数学学习评价的认识:
①通过考查学生的知识技能就可以对学生的数学学习进行全面评价
②通过考查学生的情感与态度就可以对学生的数学学习水平进行评价
③数学学习的评价重在学习过程,对于学习结果不必看重
④数学学习的评价重在激励学生学习,而不是改进教师教学其中,不正确的为( )。
A、③④
B、 ①②③
C、①②④
D、①②③④
二、(本大题共5小题,每题7分,共35分)
9
设x=0.2431。请写出x的既约分数形式。
10
某人从A处开车到D处上班,若各路段发生堵车事件是相互独立的,发生堵车的概率如图2所示(例如路段Ac发生堵车的概率是1/10)。请选择一条由A到D的路线,使得发生堵车的概率最小,并计算此概率。

11
设 的三条边分别是a,b,C,且a2+b2=c2。证明:ΔABC是直角三角形。(这是勾股定理的逆命题)
的三条边分别是a,b,C,且a2+b2=c2。证明:ΔABC是直角三角形。(这是勾股定理的逆命题)
 的三条边分别是a,b,C,且a2+b2=c2。证明:ΔABC是直角三角形。(这是勾股定理的逆命题)
的三条边分别是a,b,C,且a2+b2=c2。证明:ΔABC是直角三角形。(这是勾股定理的逆命题)12
举例说明运用综合法证明数学结论的思维过程和特点。
13
简述“尺规作图”的基本要求,并写出古希腊时期“几何作图三大问题”的具体内容。
三、(本大题1小题,10分)
14
已知方程 表示的几何图形是椭圆,求出其短半轴与长半轴的长度。
表示的几何图形是椭圆,求出其短半轴与长半轴的长度。
 表示的几何图形是椭圆,求出其短半轴与长半轴的长度。
表示的几何图形是椭圆,求出其短半轴与长半轴的长度。 四、(本大题1小题,15分)
15
以初中阶段的函数概念为例,阐述数学课程内容的呈现如何体现螺旋上升的原则。
五、(本大题1小题,20分)阅读案例,并回答问题。
16
案例
下面是两位教师关于《等边三角形》的教学过程
问题:
请从下列三个方面对甲乙两位教师的教学过程进行评价:
(1)引入的特点;(6分)
(2)教师教的方式;(7分)+
(3)学生学的方式。(7分)
下面是两位教师关于《等边三角形》的教学过程
|
教师甲 |
教师乙 |
|
(1)复习等腰三角形的性质及判定方法。 教师提问、学生思考:边怎样?角怎样?对称性呢? (2)等边三角形性质的教学。 教师提问、学生思考: ①什么样的三角形叫等边三角形? ②等边三角形的三个内角都相等吗? ③等边三角形是轴对称图形吗? (3>等边三角形判定的教学 师:哪位同学说说我们应从什么角度来考虑等边三角形 的判定方法? 生:从角和边来考虑。(教师希望的答案是从边和角来考 虑) 师:那你能说一下等边三角形有怎样的判定方法吗? 生:从角来说,我认为三个内角都是600的三角形是等边 三角形(学生的回答出乎老师的预设,打乱了PPT的放 映程序) 师:关于边的研究比较简单,我们还是从边开始探讨吧。 生:好。(学生没有异议,只能跟着老师的要求回答问题, 继续学习) |
(1)复习引入 ①理解等腰三角形的定义、性质; ②观察生活中的等边三角形,引出课题。 (2)新课教学 ①等边三角形有什么性质? (PPT显示)可以从边、角、对称性来考虑 设计活动1: 学生拿出课前准备的等边三角形纸片,认真折叠并 观察,小组合作,互相探讨,一个小组代表发表自己 组的观点.其他小组补充,最后一起归纳总结。 ②等边三角形的判定方法有哪些?设计开放性提问 (唧’显示) 你认为怎样才能说明三角形是等边三角形?等腰三 角形怎样变化才能说明是等边三角形? 设计活动2: 小组合作,互相探讨,教师操作几何画板,学生也上 台操作几何画板,观察等腰三角形满足什么条件后 成为等边三角形。学生积极主动地参与课堂学习,能 够在折纸操作后很快说出等边三角形的性质和判定 方法.通过操作几何画板形象地展现变化过程。新知 识的获得和掌握很快且水到渠成,最后教师和学生 一起归纳总结。 |
问题:
请从下列三个方面对甲乙两位教师的教学过程进行评价:
(1)引入的特点;(6分)
(2)教师教的方式;(7分)+
(3)学生学的方式。(7分)
六、教学设计题(本大题共30分)
17
某位教师在讲完《相交线与平行线》这部分内容后,设计了一节《相交线与平行线》的复习课.在这节课中,他设计了如下一组题:
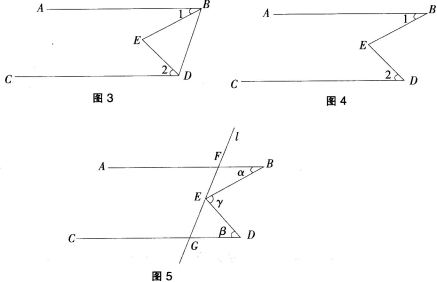
题1.如图3.BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90。。
①BE与DE有什么样的位置关系?请说明理由。
②AB与CD有什么样的位置关系?请说明理由。
题2.如图4,AB∥CD且∠1+∠2=800:,求∠BED的度数。
题3.如图5,AB∥CD直线1交AB于点F、交CD于点G,点E是线段GF上的一点(点E
与点F、G不重合),设∠ABC=β,∠BED=γ。试探索a,β、γ之间的关系,并说明理由。
阅读上述教学设计片段,完成下列任务:
(1)从这组习题分析这节复习课的教学目标;(8分)
(2)分析这三道题的设计意图,并说明这组习题设计的特点;(10分)
(3)请你在图5的基础上,编一道类似习题,并给出答案。(12分)
题1.如图3.BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90。。
①BE与DE有什么样的位置关系?请说明理由。
②AB与CD有什么样的位置关系?请说明理由。
题2.如图4,AB∥CD且∠1+∠2=800:,求∠BED的度数。
题3.如图5,AB∥CD直线1交AB于点F、交CD于点G,点E是线段GF上的一点(点E
与点F、G不重合),设∠ABC=β,∠BED=γ。试探索a,β、γ之间的关系,并说明理由。

阅读上述教学设计片段,完成下列任务:
(1)从这组习题分析这节复习课的教学目标;(8分)
(2)分析这三道题的设计意图,并说明这组习题设计的特点;(10分)
(3)请你在图5的基础上,编一道类似习题,并给出答案。(12分)